ANALYSIS II
Metric Spaces: Open and Closed Sets
Defn
If  > 0, then an open
> 0, then an open  -neighborhood
of x is defined to be the set B
-neighborhood
of x is defined to be the set B (x)
:= {y
in X | d(x,y) <
(x)
:= {y
in X | d(x,y) <  }.
This set is also referred to as the open
ball of radius
}.
This set is also referred to as the open
ball of radius  and center
x. The set {y
in X | d(x,y)
and center
x. The set {y
in X | d(x,y) 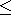
 }is
called the closed
ball, while the set {y
in X | d(x,y) =
}is
called the closed
ball, while the set {y
in X | d(x,y) =  }is
called a sphere.
}is
called a sphere.
Defn
A subset O of X is
called open if,
for each x in O,
there is an  -neighborhood of x
which is contained in O.
-neighborhood of x
which is contained in O.
Proposition
Each open  -neighborhood
in a metric space is an open set.
-neighborhood
in a metric space is an open set.
Theorem
The following holds true for the open subsets of a metric space (X,d):
- Both X and the empty set are open.
- Arbitrary unions of open sets are
open.
- Finite intersections of open sets
are open. (Homework due Wednesday)
Proposition
Suppose Y is a
subset of X, and dY is the restriction
of d to Y, then
- (Y,dY)
is a metric space and open subsets of Y are just the intersections with
Y of open subsets of X.
- if Y is open in X, a set is open
in Y if and only if it is open in X.
- in general, open subsets
relative to Y may fail to be open relative to X.
Examples:
Arbitrary intersectons of open sets need not be open:
- If On
:= (-1/n, 1/n), then
 n
On = {0}.
n
On = {0}.
- If On
:= (-1/n, 1 +1/n), then
 n
On = [0,1).
n
On = [0,1).
Defn
Suppose X is a set and T is a collection of subsets
of X with the properties
- both X and the empty set belong
to T,
- T is closed under
arbitrary unions,
- T is closed
under finite intersections,
then (X, T )
is called a topological space
and T is called a topology
for X. Moreover, each O
in T is called a neighborhood
for each of their points.
Defn
A subset C of a metric space X is called closed
if its complement is open in X.
Examples:
Each of the following is an example of a closed set:
- Each closed
 -nhbd
is a closed subset of X.
-nhbd
is a closed subset of X.
- The set {x
in R | x
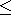 d
} is a closed subset of C.
d
} is a closed subset of C.
- Each singleton set {x} is a closed
subset of X.
- The Cantor
set is a closed subset of R.
To construct this set, start with the closed interval [0,1] and recursively
remove the open middle-third of each of the remaining closed intervals
...
At the n-th stage, we have 2n closed intervals each of length
(1/3)n :
Stage 0: [0,1]
Stage 1: [0,1/3] [2/3,1]
Stage 2: [0,1/9] [2/9,3/9] [6/9,7/9] [8/9,1]
.
.
.
This finite union of closed intervals is closed. The Cantor set is the
intersection of this (decreasing or nested) sequence of sets and so is
also closed. Later, we will see that the Cantor set has many other interesting
properties.
Homework #4 (Due Monday
01/26)
- Suppose (X,T) is
a topological space. Prove each of the following:
- Both X and empty set are
closed sets.
- Arbitrary intersections of closed
sets are closed.
- Finite unions of closed sets are
closed.
- Show that {0 , 1 , 1/2 , 1/3 ,
... , 1/n , ...} is a closed set in R and in C.
Robert Sharpley Jan 19 1998
![]() > 0, then an open
> 0, then an open ![]() -neighborhood
of x is defined to be the set B
-neighborhood
of x is defined to be the set B![]() (x)
:= {y
in X | d(x,y) <
(x)
:= {y
in X | d(x,y) < ![]() }.
This set is also referred to as the open
ball of radius
}.
This set is also referred to as the open
ball of radius ![]() and center
x. The set {y
in X | d(x,y)
and center
x. The set {y
in X | d(x,y) ![]()
![]() }is
called the closed
ball, while the set {y
in X | d(x,y) =
}is
called the closed
ball, while the set {y
in X | d(x,y) = ![]() }is
called a sphere.
}is
called a sphere.![]() -neighborhood of x
which is contained in O.
-neighborhood of x
which is contained in O. ![]() -neighborhood
in a metric space is an open set.
-neighborhood
in a metric space is an open set.