61.html

6th Funky Function:

A function that is continuous everywhere

but nowhere differentiable.

Take a Weierstrass Function

f(x) = sin ( π x)

for some fixed constants a and b

where 0 < a < 1 and ab ≥1 .
Consider the partial sums of f,

S_n (x) = sin ( π x) .

Below, let's graph, with domain [-d, d],

S_0, S_1, S_2, .... S_enough

all on the same grid in a fancy

"animated" effect with the S_n's

forming a "moving picture". I set

the speed at 1 frame per second

so it will take (enough+1) seconds to show

you S_0 through S_enough

> restart; with(plots):
a := 3/4 ;
b := 4 ;
d := 1 ;
enough := 10 ;
c := k->a^k*abs(sin(b^k*Pi*x));
S:=Sum(c(k), k=0..n);
q1:=[seq(S, n=0..enough)]:
q2:=[seq(plot(g,x=-d..d),g=q1)]:
display(q2,insequence=true);

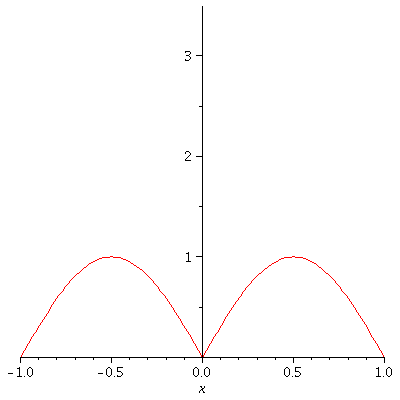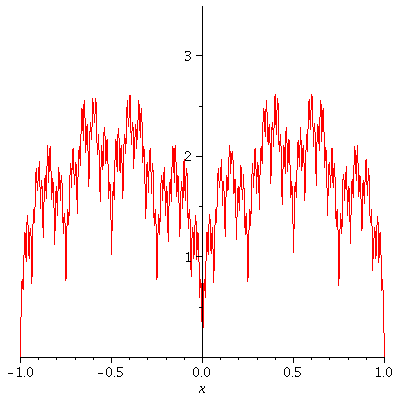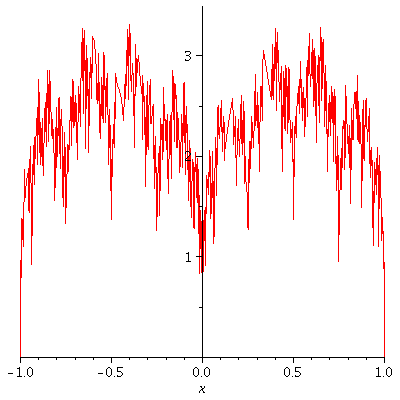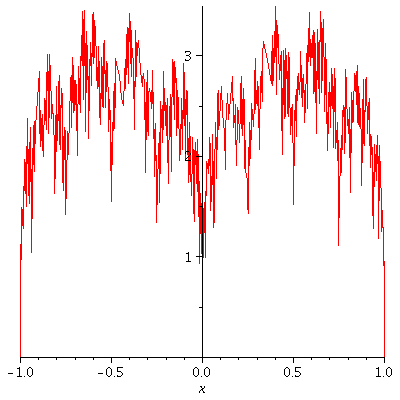Plot_2d

Let's do a "zoom" by changing the domain.

> restart; with(plots):
a := 3/4 ;
b := 4 ;
d := 0.1 ;
enough := 10 ;
c := k->a^k*abs(sin(b^k*Pi*x));
S:=Sum(c(k), k=0..n);
q1:=[seq(S, n=0..enough)]:
q2:=[seq(plot(g,x=-d..d),g=q1)]:
display(q2,insequence=true);

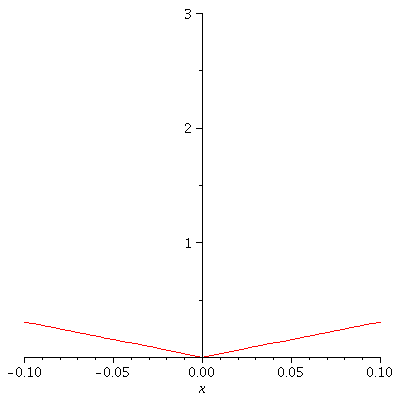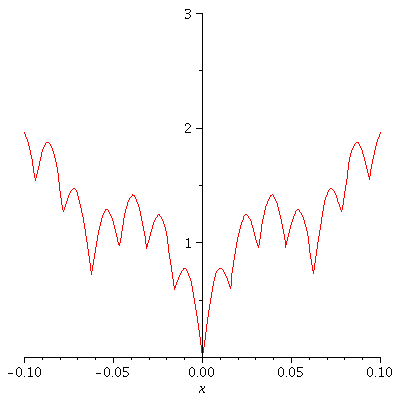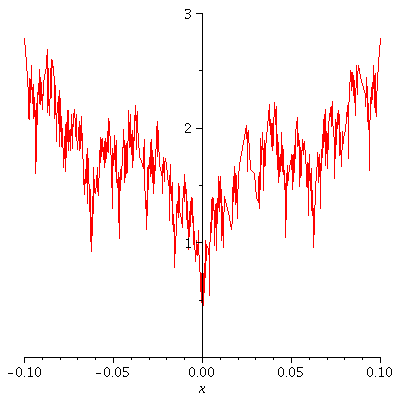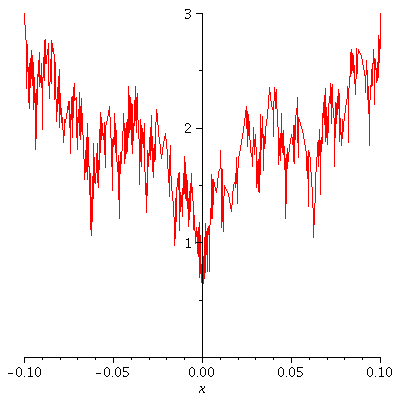Plot_2d

Here is Example 8.5.3 from Stoll's book.

> restart; with(plots):
a := 1/2 ;
b := 13 ;
d := 2;
enough := 10 ;
c := k->a^k*abs(cos(b^k*Pi*x));
S:=Sum(c(k), k=0..n);
q1:=[seq(S, n=0..enough)]:
q2:=[seq(plot(g,x=-d..d),g=q1)]:
display(q2,insequence=true);

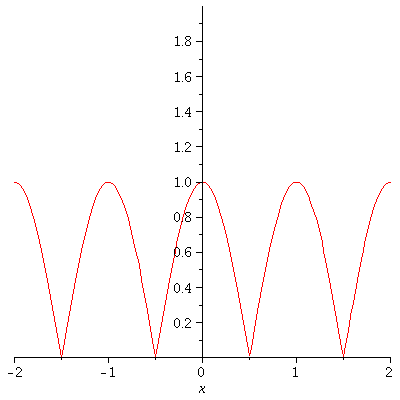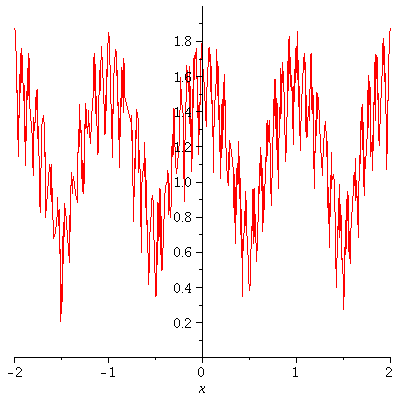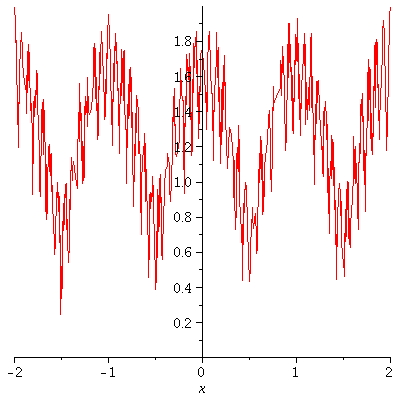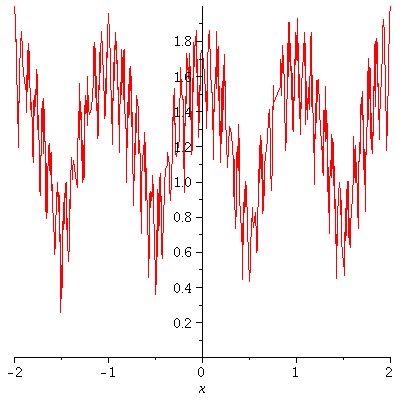Plot_2d

That's all!