if x is not zero 5th Funky Functions: C^infinity Function.
A function (that is not always zero),
infinitely often differentiable,
but the n-th derivative at zero is always zero.
Consider the function g : R --> R defined by
g(x) = if x is not zero
g(x) = 0 if x=0 .
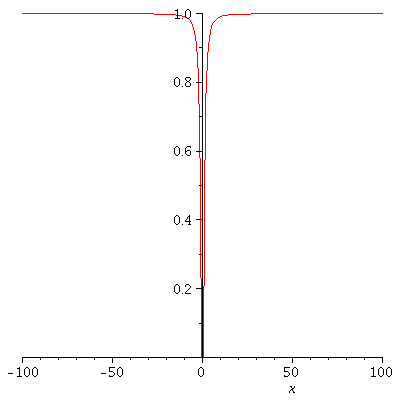
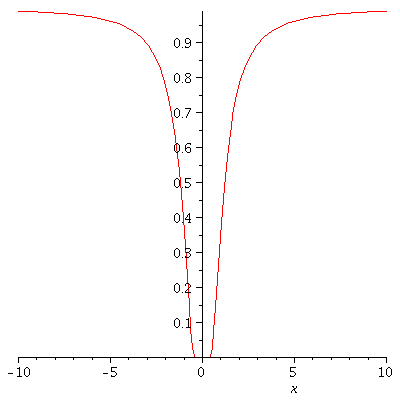
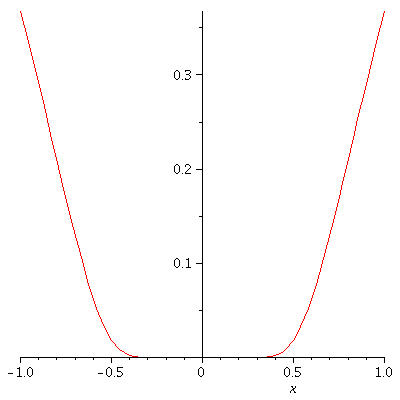
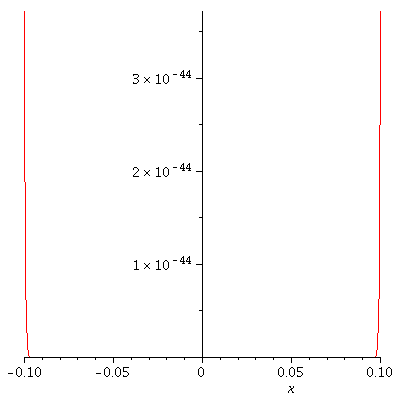
Let's look at a graph of g ...
actually, 4 graphs of g .... zooming in on x=0.
| > | restart;
g := x -> exp(-x^(-2)); plot(g(x), x= -100 ... 100); plot(g(x), x= -10 .. 10); plot(g(x), x= -1 .. 1); plot(g(x), x= -0.1 .. 0.1); |
 |
|
 |
|
 |
|
 |
|
 |
Next let's look at: g,
the first derivative 
g
of g, and
the second derivative 
g
of g.
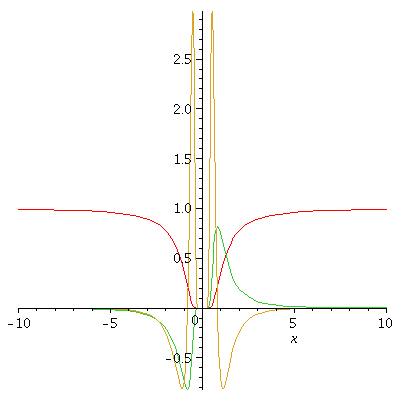
Let's first graph on the domain [-a1, +a1]
and then zoom in on zero and
graph on domain [-a2, a2] with
a restricted output [-b2, +b2] for viewing purposes.
| > | restart;
a1 := 10; a2 := 1 ; b2 := 0.00001; g := x -> exp(-x^(-2)); D1g := simplify(diff(g(x), x$1)) ; D2g := simplify(diff(g(x), x$2)) ; plot( {g(x), D1g(x), D2g(x) } , x= -a1 .. a1); plot( {g(x), D1g(x), D2g(x) } , x= -a2 .. a2, y=-b2 .. b2); |
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
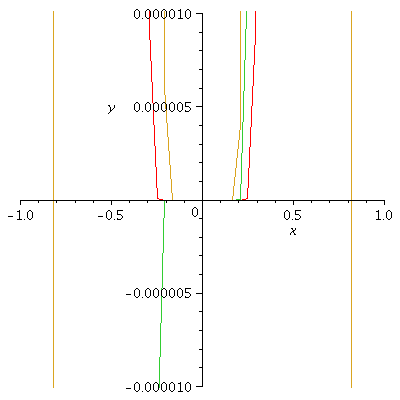Below you can investigate the derivatives of g:
g, 
g, 
g, .... 
g,
for your choice of "k" and "enough" .
There is:
1) DerOFg = sequence of the functions:
kth derivative of g, (k+1)st derivative of g, ....,
(k+ enough)th derivative of g
3) The (enough + 1) functions above,
all ploted on the same grid with domain [-a, a]
and resticted output range [-b, b] .
| > | restart;
k:= 17; enough := 3; a := .5; b := 1; g := x -> exp(-x^(-2)); DerOFg := [seq(simplify(diff(g(x), x$n)), n=k .. k+enough)]; plot(DerOFg , x= -a .. a, y=-b .. b); |
| > |
 |
|
 |
|
 |
|
 |
|
 |
|
                     |
|
 |
| > |
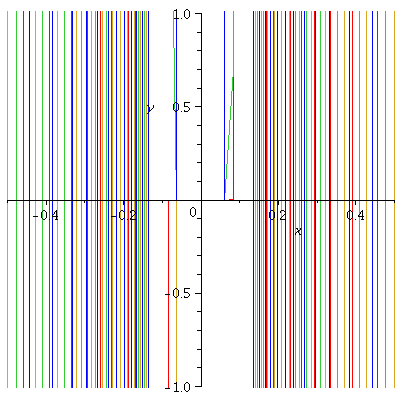That's all