4th Funky Functions: C^n Function.  

A function that is n-times differentiable,  

but not (n+1)-times differentiable  

Let n be an integer  and consider the function:  

    : [-a, +a] --> R  

    (x) =  

so  

    (x) =  

So, for some constant  

   (x) =  

which is not differentiable at x=0.  

For this example, do you really care what  

the constant  

Below you can investigate   

g_k, g_{k+1}, g_{k+2}, .... g_{k+enough}  

for your choice of "k" and "enough" .   

There is:  

1) SeqOFgn = sequence of the functions:   

g_k, g_{k+1}, g_{k+2}, .... g_{k+enough}  

2) nthDerOFgn = sequence of the functions:  

kth derivative of g_k,  (k+1)st derivative of g_(k+1), ...., until enough 

3) The functions  

g_k, g_{k+1}, g_{k+2}, .... g_{k+enough}  

all ploted on the some grid with domain [-a, a]  

>	restart;   k:= 1; enough := 3; a := .5; g := n -> (x)^(n+1/3); SeqOFgn := [seq(g(n), n=k .. k+enough)]; nthDerOFgn := [seq(diff(g(n), x$n),              n=k .. k+enough)]; plot( SeqOFgn , x= -a .. a);

 

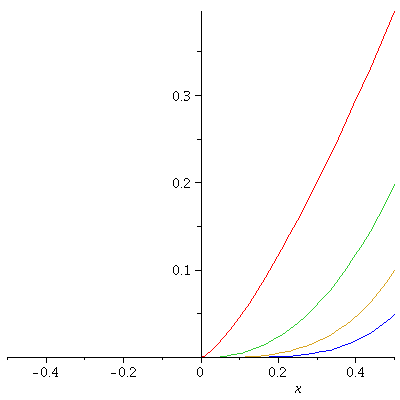*) disclaimer ....  

Maple is only giving me the plots on [0,a] ....  

by symmetry I can easily envision what  

the plot on the whole of [-a,a] looks like ....  

but I'm not going to waste time trying to figure out Maple 11 ...  

the last time I used Maple they were at Maple 4 ...   

>

 

Think about what the plot is saying.  

Why does the 1st derivative of g_1 not exist at x=0?  

Well, the derivative from the right & left  is "+ infinity",  

ie., the tangent line is trying to be vertical.   

Think about what happens each time you take  

a derivative of some derivative of a g_n  ...  

and the "steepness" of the g_n's.   

That's all.