31.html

3rd Funky Functions: C^1 Function.

A function that is differentiable,

but the derivative is not continuous.

Let b>0 and consider the function:

f : [-a, +a] --> R

f(x) = x^b sin(1/x) if x isn't 0

f(x) = 0 if x = 0 .

In Problem 5.1.13 we (basically,

due to symmetry) showed that

a) f is cont. at x=0 iff b>0

b) f is diff. at x=0 iff b>1

c) f ' is cont at 0 iff b > 2.

In the Funky Functions assignment,

the 3rd Funky Function function was

the above function f with b=2.

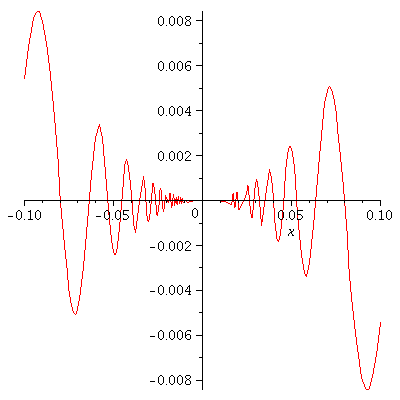
Let's see how this function f looks

on the domain [-a, +a] with b=2.

> restart;
a:= .1;
b:= 2;
f := x -> x^b*sin(1/x);
plot(f(x),x=-a..a);

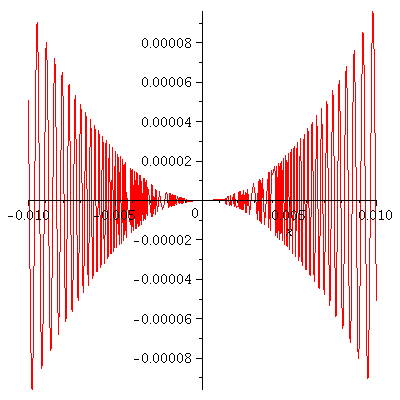
Plot_2d

Ok, now below you can mess around with

the domain [-a, a] of f as well as the b>0

and see what happens.

> restart;
a:= 0.01;
b:= 2;
f := x -> x^b*sin(1/x);
plot(f(x),x=-a..a);

Plot_2d

If you want, you can also adjust

the range (output) of the graph (plot) of f.

> restart;
a:= 0.01; d:= 0.00002;
b:= 2;
f := x -> x^b*sin(1/x);
plot(f(x),x=-a..a,y=-d..d);